Искам да напиша нещо добро за МОН...
г. 23:43 ч. Кристиан Димитров
Искам да напиша нещо добро за МОН... И за експертите по Математика в любимото Министерство на Образованието.
Не мога, заради грешните задачи, които дадоха на общински, областен и национален кръг на Олимпиадата по Математика. Не мога и заради грешно формулираната задача, с която завършиха сезона - 24Б от днешните матури за 7 клас по математика.
Поредна важна математическа проява, поредно недоглеждане, недопустимо за ученик, камо ли за експерт от Министерството. Учудва ли се някой...
Коментари от МОН най-вероятно няма да има. Поредното нещо, за което ще се мълчи. Ако се наложи... най-много някой да каже, че грешчицата не пречи задачата да бъде решена и да бъде получена заветната цифра 42, за която се дават точки.
Е... не е така, много деца са блокирали от невъзможнотo условие, ето и някои цитати от първите реакции в БГ Мама:
Не било важно, че експертите от МОН са пуснали грешна задача на НВО, понеже задачата не можело да се докаже, че е грешна със седмокласни знания...
Ама мили хора :), задачата или е правилна или е неправилна. Проблемът е, че тези, които съставят темите трябва да разполагат с повечко от седмокласни знания!
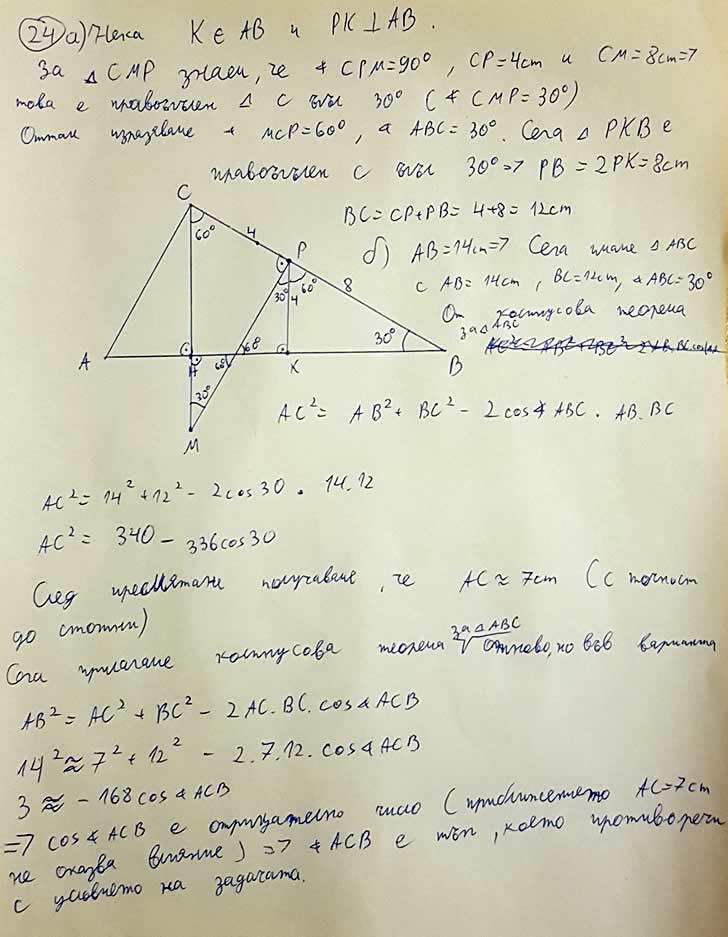
Започвам с условието на невъзможната задача 24: А ето и доказателство, че е невъзможно:
А ето и доказателство, че е невъзможно:
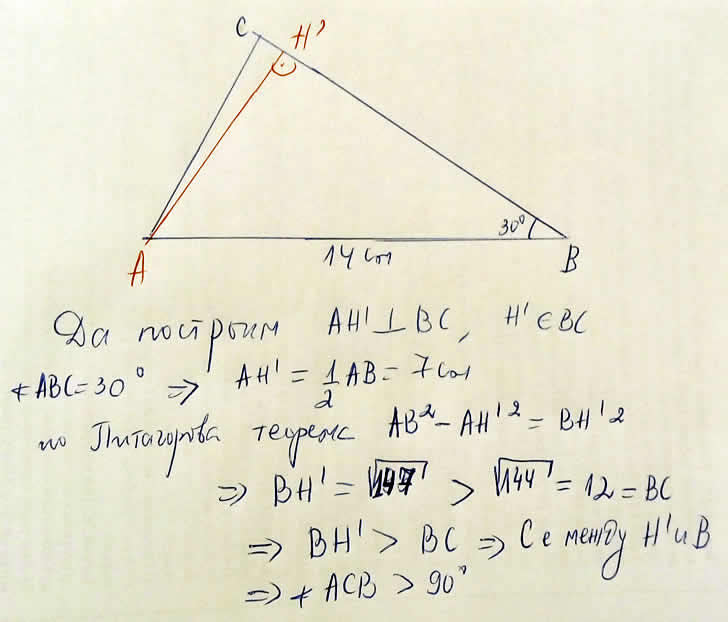
За това доказателство се използва Питагорова Теорема. Искам да ви уверя, че надали има дете в 7, да не кажа и в 6 клас от математическа гимназия, което да не е запознато с нея и не я използва. Което е достатъчна причина един добър математик да изпадне в паника при така зададена задача и да не може да я реши по напълно обективни причини, произтичащи от грешки на експертите от МОН, а не от пропуски в знанията му.
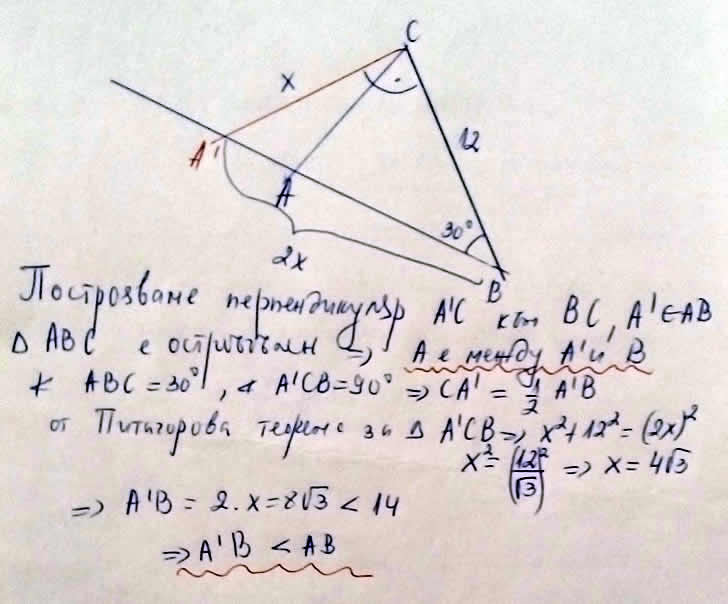
Искате още, различни решения? Ето още едно:
Тезата - няма значение, че задачата е грешна, тя не е повлияла на децата просто не е вярна. Точно на най-добрите деца има вероятност да повлияе най-много...
И един пример от БГМама със задача, подходяща за 1 клас:
Даден е триъгълник със страни 10 см., 2см. и 1см. Намерете обиколката му.
Отговор: 13 см.
Тази задача коректна ли е??? Че е решима, решима е...
Докъде стигнахме...
Задача за НВО е грешна. Всеки приема, че е така, но спорът е има ли това значение или няма. :(
#НВО 2017 #НВО математика #грешка НВО #24 задача НВО #МОН
Искам... ама нямам желание
Или по-точно не мога. Заради хаоса, който съпътстваше тази учебна година всички състезания.Не мога, заради грешните задачи, които дадоха на общински, областен и национален кръг на Олимпиадата по Математика. Не мога и заради грешно формулираната задача, с която завършиха сезона - 24Б от днешните матури за 7 клас по математика.

Поредна важна математическа проява, поредно недоглеждане, недопустимо за ученик, камо ли за експерт от Министерството. Учудва ли се някой...
Коментари от МОН най-вероятно няма да има. Поредното нещо, за което ще се мълчи. Ако се наложи... най-много някой да каже, че грешчицата не пречи задачата да бъде решена и да бъде получена заветната цифра 42, за която се дават точки.
Е... не е така, много деца са блокирали от невъзможнотo условие, ето и някои цитати от първите реакции в БГ Мама:
Мерила е и с транспортир и с линия и е чертала перпендикуляри с пергел... и при всеки неуспех е упреквала себе си, че някъде греши... и като не може да си ситуира правилно чертежа изобщо не е посмяла да решава нататъка по него!
Абсолютно същото нещо е станало и с моето дете. Блокирал е на чертежа и така нищо не е направил на задачата.
Синът ми каза, че е бил на крачка да напише, че задачата няма решение - 24-та. Мъчил се точно заради условието за остроъгълен триъгълник. Решавал, решавал и бил в патова ситуация. В крайна сметка задачата е изгубена, май някакъв ъгъл му се получил.
Тя излиза от училище и се тресе от рев - зациклила един час и 10 минути на 24 задача. Правила дванадесет чертежа, изпаднала в шок и ужас и между другото се овладяла накрая да пренесе верните отговори на 21, 22, 23 и половината от 24. Е, ако и това не беше се случило, щях да хода да …… Искам справедливост!!!
И като не могат да си го представят как да решат задачата? Защо изобщо е трябвало да се пише че е остроъгълен, не ми е ясно, но е факт, че е написано и това прави задачата невъзможна за решаване.
Приблизително 91 градуса се получава "острият" ъгъл, ако АБ е 14 см.
Има условие за остроъгълен триъгълник. В окончателното решение триъгълника не отговаря на това условие и следователно той не е решение на задачата.
Децата, които са разбрали за проблема в задачата, трябва да бъдат поощрени. Моето дете иска да учи с смг, дали е честно да изгуби едни 6 точки, заради неточност в задачата. На черновата има записана дължината на ВС -12см., както и двата ъгъла по 30 градуса
Имат линия и транспортир и да, чертаят с точност до милиметър, замерват ъгъла и установяват, че триъгълника не е остроъгълен. И го отхвърлят като решение.
В резултат на което не са търсили въобще лицето му. Нима такова дете заслужава да бъде резнато за цяло подусловие, защото не е намерило автоматично полупроизведението на 14 и 6..
Последната задача не ми излиза и не ми излиза... Направих два чертежа и не става.. Накрая толкова се притесних, че се наложи с лявата ръка да стискам дясната, за да спре да се тресе и да продължа да опитвам.
Господа от МОН, този стрес, който причинихте на детето ми, с никакви точки не може да го компенсирате!
Редакция 23 май
В онлайн пространство се завихри някаква странна дискусия...Не било важно, че експертите от МОН са пуснали грешна задача на НВО, понеже задачата не можело да се докаже, че е грешна със седмокласни знания...
Ама мили хора :), задачата или е правилна или е неправилна. Проблемът е, че тези, които съставят темите трябва да разполагат с повечко от седмокласни знания!
Информация и новини за Министерство на образованиетоЗа хората, влагащи като оправдаващо неточността обстоятелство невъзможността да се докаже от седмокласник, че триъгълникът е тъпоъгълен при зададено условие да е остроъгълен... ето едно доказателство, напълно по силите на седмокласник, обучавал се в математическите гимназии в България.
Започвам с условието на невъзможната задача 24:
 А ето и доказателство, че е невъзможно:
А ето и доказателство, че е невъзможно:

За това доказателство се използва Питагорова Теорема. Искам да ви уверя, че надали има дете в 7, да не кажа и в 6 клас от математическа гимназия, което да не е запознато с нея и не я използва. Което е достатъчна причина един добър математик да изпадне в паника при така зададена задача и да не може да я реши по напълно обективни причини, произтичащи от грешки на експертите от МОН, а не от пропуски в знанията му.
Искате още, различни решения? Ето още едно:

Идеята не е да се докаже по време на НВО, че задачата е грешна, а това, че някои деца могат да разберат, че в условието има нещо нередно
Естествено е да предположат, че грешката е в тях, а не в експертите, изготвили темата, а това най-малко ще им наруши концентрацията и ще доведе до притеснения, които мога да се изразят в грешен отговор на тази задача и в загуба на много време за обмисляне на друго, несъществуващо решение...Тезата - няма значение, че задачата е грешна, тя не е повлияла на децата просто не е вярна. Точно на най-добрите деца има вероятност да повлияе най-много...
И един пример от БГМама със задача, подходяща за 1 клас:
Даден е триъгълник със страни 10 см., 2см. и 1см. Намерете обиколката му.
Отговор: 13 см.
Тази задача коректна ли е??? Че е решима, решима е...
Докъде стигнахме...
Задача за НВО е грешна. Всеки приема, че е така, но спорът е има ли това значение или няма. :(
Споделете вашето мнение по темата във форума ни
Информация, новини, задачи и решения от Матура по математика - НВО за седмокласници
Споделете тази новина:
Още интересно от AlekDimitrov.com:
Последни Новини
• Втори математически турнир Ключът към знанието
• Школа по математика Олимпийци - курсове 2023 / 2024
• Първи математически турнир Ключът към знанието!
• Курсове по математика в Школа Олимпийци
• Марияна Влъчкова - Завинаги в мислите ни.
• Стажантска програма в училище ЕСПА
• Стартира записването за курсовете в Сикадеми през учебната 2021/2022
• Обновени класации на софийските училища спрямо резултати от НВО / матури
• Онлайн курс по състезателна математика за математици от 8 до 12 клас през януари и февруари
• Ментори на кандидатстващи в Кеймбридж тази година от CantaBulgarian.

Календар на състезанията
Състезания по математика през:

Ваканции 2020 - 2021 година
Ученически Ваканции
Есенна ваканция: 30 окт. - 1 ное. 2020 г.
Коледна ваканция: 24 дек. 2020 - 3 яну. 2021 г.
Зимна / междусрочна ваканция: 30 яну. - 3 фев. 2021 г.
Пролетна ваканция 1-11 кл.: 3 - 11 април 2021 г.
Пролетна ваканция 12 клас: 8 - 11 април 2021 г.
21 май 2021 г. – Втори ДЗИ за 12 клас
24 - 25 май 2021 г. - по повод Деня на славянската писменост и българската просвета и култура
4 - 6 клас - 14 юни 2021 г.
4 - 6 клас - паралелки в спортни училища - 30 юни 2021 г.
7 - 11 клас - 30 юни 2021 г.
12 клас - 14 май 2021 г.
Коледна ваканция: 24 дек. 2020 - 3 яну. 2021 г.
Зимна / междусрочна ваканция: 30 яну. - 3 фев. 2021 г.
Пролетна ваканция 1-11 кл.: 3 - 11 април 2021 г.
Пролетна ваканция 12 клас: 8 - 11 април 2021 г.
Неучебни дни
19 май 2021 г. – Матура по БЕЛ в 12 клас21 май 2021 г. – Втори ДЗИ за 12 клас
24 - 25 май 2021 г. - по повод Деня на славянската писменост и българската просвета и култура
Край на учебната година
1 - 3 клас - 31 май 2021 г.4 - 6 клас - 14 юни 2021 г.
4 - 6 клас - паралелки в спортни училища - 30 юни 2021 г.
7 - 11 клас - 30 юни 2021 г.
12 клас - 14 май 2021 г.

Празници и Почивни Дни 2026
Официални празници. Неработни дни. Кога отработваме? Как да комбинираме неработните дни с ваканцията на детето и състезанията по математика за да планираме перфектната семейна почивка?

